Medidas de Dispersión
También llamada Medidas de Variabilidad, muestran la variabilidad de una distribución, indicando por medio de un número, si las diferentes puntuaciones de una variable están muy alejadas de la media. Cuánto mayor sea ese valor, mayor será la variabilidad, cuanto menor sea, más homogénea será a la media. Así se sabe si todos los casos son parecidos o varían mucho entre ellos.
Rango
El rango o recorrido interarticular es la diferencia entre el valor máximo y el valor mínimo en un grupo de números aleatorios. Se le suele simbolizar con ''R''
- Requisitos del rango
- Ordenamos los números según su tamaño.
- Restamos el valor mínimo del valor máximo

- Nota: Explicación Mas Amplia
- La varianza y desviación estándar (o cualquier otra medida de dispersión) indican el grado en que están dispersos los datos en una distribución. A mayor medida, mayor dispersión.
- La varianza es un número muy grande con respecto a las observaciones, por lo que con frecuencia se vuelve difícil para trabajar.
- Debido a que las desviaciones son elevadas al cuadrado y la varianza siempre se expresa en términos de los datos originales elevados al cuadrado, se obtiene unidades de medida de los datos que no tiene sentido o interpretación lógica. Por ejemplo, si se calcula la varianza de una distribución de datos medidos en metros, segundos, dólares, entre otros, se obtendrá una varianza mediada en metros cuadrados, segundos cuadrados, dólares cuadrados, respectivamente, unidades de medida que no tienen significado lógico respecto a los datos originales.
- Para solucionar las complicaciones que se tiene con la varianza, se halla la raíz cuadrada de la misma, es decir, se calcula la desviación estándar, la cual es un número pequeño expresado en unidades de los datos originales y que tiene un significado lógico respeto a los mismos.



*Ejemplo:
Para la muestra (8, 7, 6, 9, 4, 5), el dato menor es 4 y el dato mayor es 9. Sus valores se encuentran en un rango de:
Desviación Media(MD)
La desviación media o desviación promedio es la media aritmética de los valores absolutos de las desviaciones respecto a la media aritmética.
PROPIEDADES
Guarda las mismas dimensiones que las observaciones. La suma de valores absolutos es relativamente sencilla de calcular, pero esta simplicidad tiene un inconveniente: Desde el punto de vista geométrico, la distancia que induce la desviación media en el espacio de observaciones no es la natural (no permite definir ángulos entre dos conjuntos de observaciones). Esto hace que sea muy engorroso trabajar con ella a la hora de hacer inferencia a la población.
Cuando mayor sea el valor de la desviación media, mayor es la dispersión de los datos. Sin embargo, no proporciona una relación matemática precisa entre su magnitud y la posición de un dato dentro de una distribución.
La desviación media al tomar los valores absolutos mide una observación sin mostrar si la misma está por encima o por debajo de la media aritmética.
Métodos De Calculo
*Para Datos No Agrupados
Se emplea la ecuación:
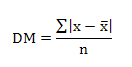
Ejemplo ilustrativo:
Calcular la desviación media de la distribución: 3, 8, 8, 8, 9, 9, 9, 18
Solución:
Se calcula la media aritmética.
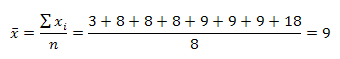
Se calcula la desviación media.
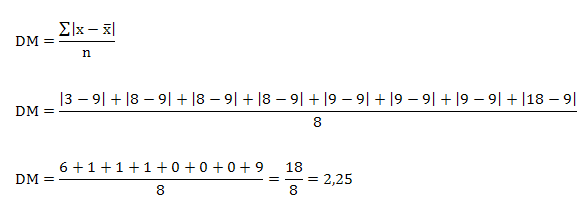
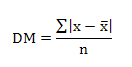
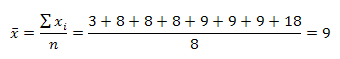
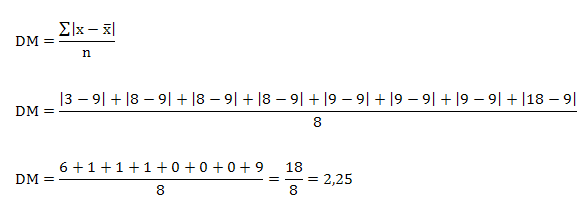
*Para Datos Agrupados en Tablas de Frecuencia
Se emplea la ecuación:

Ejemplo ilustrativo:
Calcular la desviación media en base a la siguiente tabla sobre las calificaciones de un estudiante en 12 asignaturas evaluadas sobre 10.

Calificación
|
Cantidad de asignaturas
| |
6
|
4
| |
7
|
2
| |
8
|
3
| |
9
|
2
| |
10
|
1
| |
Total
|
12
| |
Solución:
Se calcula la media aritmética.

*Para Datos Agrupados en Intervalos
Se emplea la ecuación:
 Donde xm es la marca de clase.
Donde xm es la marca de clase.

Ejemplo ilustrativo:
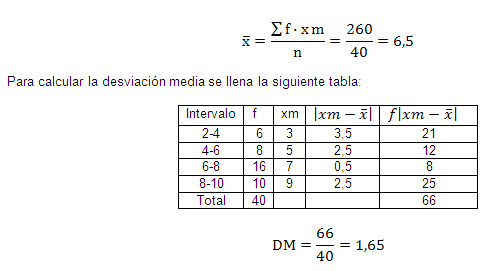
Calcular la desviación media de un curso de 40 estudiantes en la asignatura de Estadística en base a la siguiente tabla:
Calificación
|
Cantidad de estudiantes
| |
2-4
|
6
| |
4-6
|
8
| |
6-8
|
16
| |
8-10
|
10
| |
Total
|
40
| |
Solución:
Para calcular la media aritmética se llena la siguiente tabla:
Intervalo
|
f
|
xm
|
f·xm
| |
2-4
|
6
|
3
|
18
| |
4-6
|
8
|
5
|
40
| |
6-8
|
16
|
7
|
112
| |
8-10
|
10
|
9
|
90
| |
Total
|
40
|
260
| ||
Calculando la media aritmética se obtiene:
*Varianza y desviación estándar
La varianza es la media aritmética de los cuadrados de las desviaciones respecto a la media aritmética, es decir, es el promedio de las desviaciones de la media elevadas al cuadrado. La desviación estándar o desviación típica es la raíz de la varianza.
La varianza y la desviación estándar proporcionan una medida sobre el punto hasta el cual se dispersan las observaciones alrededor de su media aritmética.
*PROPIEDADES
A pesar de lo anterior, es difícil describir exactamente qué es lo que mide la desviación estándar. Sin embargo, hay un resultado útil, que lleva el nombre del matemático ruso Pafnuty Lvovich Chebyshev, y se aplica a todos los conjuntos de datos. Este teorema de Chebyshev establece que para todo conjunto de datos, por lo menos 1- 1/k2 de las observaciones están dentro de k desviaciones estándar de la media, en donde k es cualquier número mayor que 1. Este teorema se expresa de la siguiente manera:
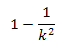 Así por ejemplo, si se forma una distribución de datos con k =3 desviaciones estándar por debajo de la media hasta 3 desviaciones estándar por encima de la media, entonces por lo menos
Así por ejemplo, si se forma una distribución de datos con k =3 desviaciones estándar por debajo de la media hasta 3 desviaciones estándar por encima de la media, entonces por lo menos
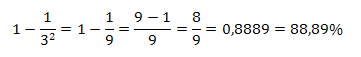 Interpretación: El 88,89% de todas las observaciones estarán dentro ± 3 desviaciones de la media.
Interpretación: El 88,89% de todas las observaciones estarán dentro ± 3 desviaciones de la media.
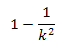
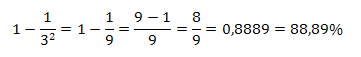
* MÉTODOS DE CÁLCULO
*Para Datos No Agrupados
La varianza para una población se calcula con:
 Notas:
Notas:
1) Para el cálculo de la varianza de una muestra se divide por n-1 en lugar de N, debido a que se tiene n-1 grados de libertad en la muestra. Otra razón por la que se divide por n-1 es debido a que una muestra generalmente está un poco menos dispersa que la población de la cual se tomó. Al dividir para n-1 en lugar de N se cumple con la tendencia y sentido lógico de que la varianza y desviación estándar de la muestra deben tener un valor más pequeño que la varianza y desviación estándar de la población.
2) En la realidad, salvo indicación expresa, no se calcula la varianza y la desviación estándar de la población, ya que para ahorrar tiempo, esfuerzo, dinero, etc. es mejor trabajar con datos que representan a la muestra.
Ejemplo ilustrativo N° 1
Considere que los siguientes datos corresponden al sueldo de una población: $350, $400, $500, $700 y $1000
1) Calcular la desviación estándar.
2) ¿Cuál es el intervalo que está dentro de k = 2 desviaciones estándar de la media?. ¿Qué porcentaje de las observaciones se encuentran dentro de ese intervalo?
Solución:
1) Para la calcular la desviación estándar se sigue los siguientes pasos:
a) Se calcula la media aritmética.
 b) Se aplica la respectiva fórmula para calcular la varianza
b) Se aplica la respectiva fórmula para calcular la varianza
 c) Se calcula la desviación estándar.
c) Se calcula la desviación estándar.

2) Cálculo del intervalo de k = 2 desviaciones estándar de la media.
Se transportan 2 desviaciones estándar (2 x $ 237,4868) = $ 474,97 por encima y por debajo de la media  = $ 590
Por lo tanto se tiene un intervalo desde $ 590 - $474,97 = $ 115,03 hasta $ 590 + $474,97 = $ 1064,97
Aplicando el Teorema de Chebyshev
= $ 590
Por lo tanto se tiene un intervalo desde $ 590 - $474,97 = $ 115,03 hasta $ 590 + $474,97 = $ 1064,97
Aplicando el Teorema de Chebyshev
 Interpretación: Se puede afirmar de que por lo menos el 75% los sueldos están entre $ 115,03 y $ 1064,97
Interpretación: Se puede afirmar de que por lo menos el 75% los sueldos están entre $ 115,03 y $ 1064,97
Ejemplo ilustrativo N° 2:
Dos empresas, A y B, venden sobres de café instantáneo de 350 gramos. Se seleccionaron al azar en los mercados cinco sobres de cada una de las compañías y se pesaron cuidadosamente sus contenidos. Los resultados fueron los siguientes.




 = $ 590
= $ 590
A
|
B
|
350,14
|
350,09
|
350,18
|
350,12
|
349,98
|
350,20
|
349,99
|
349,88
|
350,12
|
349,95
|
1) ¿Qué empresa proporciona más café en sus sobres?
2) ¿Qué empresa llena sus sobres de manera más consistente?
Solución:
a) Se calcula las medias aritméticas.

Interpretación:
Como la media aritmética de la empresa A es mayor que la de la empresa B, por lo tanto la empresa A proporciona más café en sus sobres.
b) Se calcula las desviaciones estándar.

Interpretación:
Como la desviación estándar de la empresa A es menor a la desviación estándar de la empresa B, por lo tanto la empresa A es más consistente al llenar los sobres de café.
* Para Datos Agrupados en Tablas de Frecuencia
La varianza para una población se calcula con:
 Ejemplo ilustrativo:
Ejemplo ilustrativo:
Calcular la desviación estándar de los siguientes datos correspondientes a una muestra.

Calificaciones
|
f
|
4
|
3
|
5
|
6
|
6
|
4
|
7
|
13
|
8
|
7
|
10
|
6
|
Total
|
39
|
Solución:
a) Se llena la siguiente tabla:
Calificaciones
|
f
|
fx
|
4
|
3
|
12
|
5
|
6
|
30
|
6
|
4
|
24
|
7
|
13
|
91
|
8
|
7
|
56
|
10
|
6
|
60
|
Total
|
39
|
273
|
b) Se calcula la media aritmética.

* Para Datos Agrupados en Intervalos
La varianza para una población se calcula con:
 Ejemplo ilustrativo:
Ejemplo ilustrativo:
Calcular la desviación estándar de los siguientes datos correspondientes a una muestra.

Intervalo
|
f
|
60-65
|
5
|
65-70
|
20
|
70-75
|
40
|
80-85
|
27
|
85-90
|
8
|
Total
|
100
|
Solución:
a) Se llena la siguiente tabla:
Intervalo
|
f
|
xm
|
f·xm
|
60-65
|
5
|
62,5
|
312,5
|
65-70
|
20
|
67,5
|
1350
|
70-75
|
40
|
72,5
|
2900
|
80-85
|
27
|
82,5
|
2227,5
|
85-90
|
8
|
87,5
|
700
|
Total
|
100
|
7490
|
b) Se calcula la media aritmética.

d) Se calcula la desviación estándar.

Rango Intercuartílico
El rango intercuartílico es una medida de variabilidad adecuada cuando la medida de posición central empleada ha sido la mediana. Se define como la diferencia entre el tercer cuartil (Q3) y el primer cuartil (Q1), es decir: RQ = Q3 - Q1. A la mitad del rango intercuartil se le conoce como desviación cuartil (DQ): DQ = RQ/2= (Q3 - Q1)/2.
Se usa para construir los diagramas de caja y bigote (box plots) que sirven para visualizar la variabilidad de una variable y comparar distribuciones de la misma variable; además de ubicar valores extremos.
En estadística descriptiva, se le llama rango intercuartílico o rango intercuartil, a la diferencia entre el tercer y el primer cuartil de una distribución. Es una medida de la dispersión estadística.
A diferencia del rango, se trata de un estadístico robusto.
*Forma De Calcular
Se obtiene al evaluar:
Q3 - Q1
Donde:
Q3 es cuartil tercero
Q1 es cuartil primero.
Se obtiene al evaluar:
Q3 - Q1
Donde:
Q3 es cuartil tercero
Q1 es cuartil primero.
Rango Interpercentilico
Desviación Estándar(Típico)
La desviación estándar o desviación típica (denotada con el símbolo σ o s, dependiendo de la procedencia del conjunto de datos) es una medida de dispercion para variables de razón (variables cuantitativas o cantidades racionales) y de intervalo. Se define como la raíz cuadrada de la varianza de la variable.
Para conocer con detalle un conjunto de datos, no basta con conocer las medidas de tendencia central, sino que necesitamos conocer también la desviación que presentan los datos en su distribución respecto de la media aritmética de dicha distribución, con objeto de tener una visión de los mismos más acorde con la realidad al momento de describirlos e interpretarlos para la toma de decisiones.
Interpretación Y Aplicación
La desviación típica es una medida del grado de dispersión de los datos con respecto al valor promedio. Dicho de otra manera, la desviación estándar es simplemente el "promedio" o variación esperada con respecto a la media aritmética.
Por ejemplo, las tres muestras (0, 0, 14, 14), (0, 6, 8, 14) y (6, 6, 8, 8) cada una tiene una media de 7. Sus desviaciones estándar muestrales son 7, 5 y 1r espectivamente. La tercera muestra tiene una desviación mucho menor que las otras dos porque sus valores están más cerca de 7.
La desviación estándar puede ser interpretada como una medida de incertidumbre. La desviación estándar de un grupo repetido de medidas nos da la precisión de éstas. Cuando se va a determinar si un grupo de medidas está de acuerdo con el modelo teórico, la desviación estándar de esas medidas es de vital importancia: si la media de las medidas está demasiado alejada de la predicción (con la distancia medida en desviaciones estándar), entonces consideramos que las medidas contradicen la teoría. Esto es coherente, ya que las mediciones caen fuera del rango de valores en el cual sería razonable esperar que ocurrieran si el modelo teórico fuera correcto. La desviación estándar es uno de tres parámetros de ubicación central; muestra la agrupación de los datos alrededor de un valor central (la media o promedio).
Desglose
La desviación estándar (DS/DE), también llamada desviación típica, es una medida de dispersión usada en estadística que nos dice cuánto tienden a alejarse los valores concretos del promedio en una distribución. De hecho, específicamente, el cuadrado de la desviación estándar es "el promedio del cuadrado de la distancia de cada punto respecto del promedio". Se suele representar por una S o con la letra sigma,  .
La desviación estándar de un conjunto de datos es una medida de cuánto se desvían los datos de su media. Esta medida es más estable que el recorrido y toma en consideración el valor de cada dato.
.
La desviación estándar de un conjunto de datos es una medida de cuánto se desvían los datos de su media. Esta medida es más estable que el recorrido y toma en consideración el valor de cada dato.
La desviación estándar (DS/DE), también llamada desviación típica, es una medida de dispersión usada en estadística que nos dice cuánto tienden a alejarse los valores concretos del promedio en una distribución. De hecho, específicamente, el cuadrado de la desviación estándar es "el promedio del cuadrado de la distancia de cada punto respecto del promedio". Se suele representar por una S o con la letra sigma,  .
.
 .
.
La desviación estándar de un conjunto de datos es una medida de cuánto se desvían los datos de su media. Esta medida es más estable que el recorrido y toma en consideración el valor de cada dato.
*Distribución de probabilidad continua
Es posible calcular la desviación estándar de una variable aleatoria continua como la raíz cuadrada de la integral
donde
Es posible calcular la desviación estándar de una variable aleatoria continua como la raíz cuadrada de la integral
donde
*Distribución de probabilidad discreta
La Desviación Estándar es la raíz cuadrada de la varianza de la distribución de probabilidad discreta:
Cuando los casos tomados son iguales al total de la población se aplica la fórmula de desviación estándar poblacional. Así la varianza es la media de los cuadrados de las diferencias entre cada valor de la variable y la media aritmética de la distribución.
Aunque esta fórmula es correcta, en la práctica interesa el realizar inferencias poblacionales, por lo que en el denominador en vez de  , se usa
, se usa  según la corrección de Bessel. Esta ocurre cuando la media de muestra se utiliza para centrar los datos, en lugar de la media de la población. Puesto que la media de la muestra es una combinación lineal de los datos, el residual a la muestra media se extiende más allá del número de grados de libertad por el número de ecuaciones de restricción —en este caso una—. Dado esto a la muestra así obtenida de una muestra sin el total de la población se le aplica esta corrección con la fórmula desviación estándar muestral.
según la corrección de Bessel. Esta ocurre cuando la media de muestra se utiliza para centrar los datos, en lugar de la media de la población. Puesto que la media de la muestra es una combinación lineal de los datos, el residual a la muestra media se extiende más allá del número de grados de libertad por el número de ecuaciones de restricción —en este caso una—. Dado esto a la muestra así obtenida de una muestra sin el total de la población se le aplica esta corrección con la fórmula desviación estándar muestral.

La Desviación Estándar es la raíz cuadrada de la varianza de la distribución de probabilidad discreta:
Cuando los casos tomados son iguales al total de la población se aplica la fórmula de desviación estándar poblacional. Así la varianza es la media de los cuadrados de las diferencias entre cada valor de la variable y la media aritmética de la distribución.
Aunque esta fórmula es correcta, en la práctica interesa el realizar inferencias poblacionales, por lo que en el denominador en vez de  , se usa
, se usa  según la corrección de Bessel. Esta ocurre cuando la media de muestra se utiliza para centrar los datos, en lugar de la media de la población. Puesto que la media de la muestra es una combinación lineal de los datos, el residual a la muestra media se extiende más allá del número de grados de libertad por el número de ecuaciones de restricción —en este caso una—. Dado esto a la muestra así obtenida de una muestra sin el total de la población se le aplica esta corrección con la fórmula desviación estándar muestral.
según la corrección de Bessel. Esta ocurre cuando la media de muestra se utiliza para centrar los datos, en lugar de la media de la población. Puesto que la media de la muestra es una combinación lineal de los datos, el residual a la muestra media se extiende más allá del número de grados de libertad por el número de ecuaciones de restricción —en este caso una—. Dado esto a la muestra así obtenida de una muestra sin el total de la población se le aplica esta corrección con la fórmula desviación estándar muestral.
 , se usa
, se usa  según la corrección de Bessel. Esta ocurre cuando la media de muestra se utiliza para centrar los datos, en lugar de la media de la población. Puesto que la media de la muestra es una combinación lineal de los datos, el residual a la muestra media se extiende más allá del número de grados de libertad por el número de ecuaciones de restricción —en este caso una—. Dado esto a la muestra así obtenida de una muestra sin el total de la población se le aplica esta corrección con la fórmula desviación estándar muestral.
según la corrección de Bessel. Esta ocurre cuando la media de muestra se utiliza para centrar los datos, en lugar de la media de la población. Puesto que la media de la muestra es una combinación lineal de los datos, el residual a la muestra media se extiende más allá del número de grados de libertad por el número de ecuaciones de restricción —en este caso una—. Dado esto a la muestra así obtenida de una muestra sin el total de la población se le aplica esta corrección con la fórmula desviación estándar muestral.
*Ejemplo:
Aquí se muestra cómo calcular la desviación estándar de un conjunto de datos. Los datos representan la edad de los miembros de un grupo de niños: { 4, 1, 11, 13, 2, 7 }
1. Calcular el promedio o media aritmética  .
.
 .
.
En este caso, N = 6:

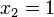




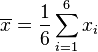 Sustituyendo N por 6
Sustituyendo N por 6
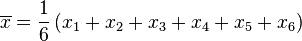


2. Calcular la desviación estándar 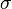

 Sustituyendo N por 6;
Sustituyendo N por 6;
 Sustituyendo
Sustituyendo 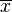 por 6,33
por 6,33
![\sigma = \sqrt{\frac{1}{5} \left [ (4 - 6,33)^2 + (1 - 6,33)^2 + (11 - 6,33)^2 + (13 - 6,33)^2 +(2 - 6,33)^2 + (7 - 6,33)^2 \right ] }](http://upload.wikimedia.org/math/1/5/c/15c8aa1bfade5b9436d186b11b2c04b0.png)
![\sigma = \sqrt{\frac{1}{5} \left [ (-2,33)^2 + (-5,33)^2 + 4,67^2 + 6,67^2 + (-4,33)^2 + 0,67^2 \right ] }](http://upload.wikimedia.org/math/0/3/a/03a16df6f28dc3cadbdae3393fe43bfb.png)



 .
.
Aquí se muestra cómo calcular la desviación estándar de un conjunto de datos. Los datos representan la edad de los miembros de un grupo de niños: { 4, 1, 11, 13, 2, 7 }
1. Calcular el promedio o media aritmética 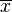 .
.
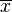 .
. .
.
En este caso, N = 6:

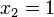




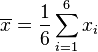 Sustituyendo N por 6
Sustituyendo N por 6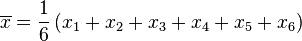


2. Calcular la desviación estándar 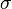
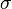

 Sustituyendo N por 6;
Sustituyendo N por 6; Sustituyendo
Sustituyendo 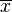 por 6,33
por 6,33![\sigma = \sqrt{\frac{1}{5} \left [ (4 - 6,33)^2 + (1 - 6,33)^2 + (11 - 6,33)^2 + (13 - 6,33)^2 +(2 - 6,33)^2 + (7 - 6,33)^2 \right ] }](http://upload.wikimedia.org/math/1/5/c/15c8aa1bfade5b9436d186b11b2c04b0.png)
![\sigma = \sqrt{\frac{1}{5} \left [ (-2,33)^2 + (-5,33)^2 + 4,67^2 + 6,67^2 + (-4,33)^2 + 0,67^2 \right ] }](http://upload.wikimedia.org/math/0/3/a/03a16df6f28dc3cadbdae3393fe43bfb.png)



 .
.Corrección De Sheppard
El calculo de la desviación tiene algo de error, debido al agrupamiento de los datos en clases (error de agrupamiento). Para ajustarnos a la realidad se utiliza la varianza corregida.

Donde ''c'' es el tamaño del intervalo de clase. La corrección introducida se conoce como CORRECCIÓN DE SHEPPARD. Se utiliza en distribuciones continuas donde las colas "colas" van gradualmente a cero en ambas direcciones.
Los estadísticos difieren en lo que se refiere a cuando y si debe aplicarse la corrección Sheppard. Ciertamente no debe aplicarse sin haber hecho un examen completo de la situación. Esto se debe a que frecuentemente se tiene a sobre corregir y así sustituir unos errores por otros.
En distintos procesamientos de datos, en ocasiones encontramos algunos problemas, ya sea en algunas clases que tengan de frecuencia a cero, pueda que esta influya a tener error al calcular la varianza, y para poder corregirla vamos a utilizar la formula que di a conocer, pues tambien se da el error al momente de calcular el intervalo y se aproxima a dos decimales, pues debe de contarse con todos los decimales o mas de dos, para que esta resulte mas confiable.
El calculo de la desviación tiene algo de error, debido al agrupamiento de los datos en clases (error de agrupamiento). Para ajustarnos a la realidad se utiliza la varianza corregida.
Los estadísticos difieren en lo que se refiere a cuando y si debe aplicarse la corrección Sheppard. Ciertamente no debe aplicarse sin haber hecho un examen completo de la situación. Esto se debe a que frecuentemente se tiene a sobre corregir y así sustituir unos errores por otros.
En distintos procesamientos de datos, en ocasiones encontramos algunos problemas, ya sea en algunas clases que tengan de frecuencia a cero, pueda que esta influya a tener error al calcular la varianza, y para poder corregirla vamos a utilizar la formula que di a conocer, pues tambien se da el error al momente de calcular el intervalo y se aproxima a dos decimales, pues debe de contarse con todos los decimales o mas de dos, para que esta resulte mas confiable.


